leetcode第52题（困难）

原链接： https://leetcode-cn.com/problems/n-queens-ii/

题目描述

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

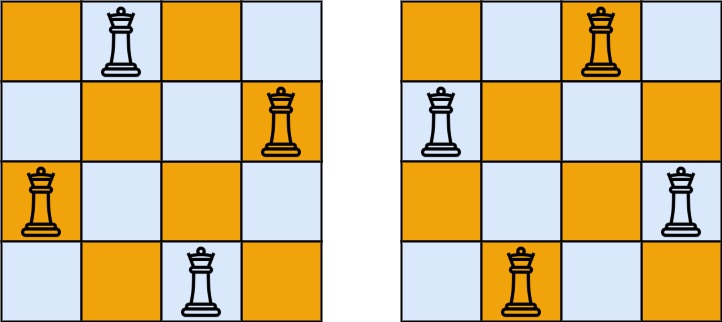
输入：n = 4，输出：2

解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1，输出：1

解题思路

1.上篇 N皇后 问题中已经解决了求解N皇后问题的所有解法并输出所有解，那么 N皇后II 并不需要返回所有解法，而是返回有多少种解法即可，这应该是N皇后问题的简化版本。在成功求出一种解法时计数器加一即可。

N皇后问题参考：http://www.jiajiajia.club/official/weblog/o1nkpk9jowzb/170

代码（java）

方式1

class Solution {
    public int totalNQueens(int n) {
        return begin(n);
    }
    int w,hh;
    boolean [] hang,lie,s,x;
    int c=0;
    public int begin(int n) {
        hang=new boolean[n];
        lie=new boolean[n];
        s=new boolean[2*n-1];
        x=new boolean[2*n-1];
        w=(hh=n)-1;
        dfs(0);
        return c;
    }
    public void dfs(int n){
        if(n>=hh){
            c++;
            return;
        }
        for (int i=0;i<hh;i++){
            int ni=n+i;
            int wi=n+(w-i);
            if(hang[i]||lie[n]||s[ni]||x[wi]){
                continue;
            }else{
                hang[i]=true;lie[n]=true;s[ni]=true;x[wi]=true;
                dfs(n+1);
                hang[i]=false;lie[n]=false;s[ni]=false;x[wi]=false;
            }
        }
    }
}

方式2（积分法）

class Solution {
public int totalNQueens(int n) {
        int[] rs = new int[]{0,1,0,0,2,10,4,40,92,352,724,2680};
        return rs[n];
    }
}