有m个人,围成一个环，编号为 1、2、3、、、m，从第一个人开始循环报数（从1开始数），假设数到n的那个人出局，然后从下一个人继续数数（从1开始数），数到n出列，以此循环，最后那个人为胜利者，求胜利者的编号，以及出局者的顺序。

        使用双向循环链表

        测试数据 m=9,n=5

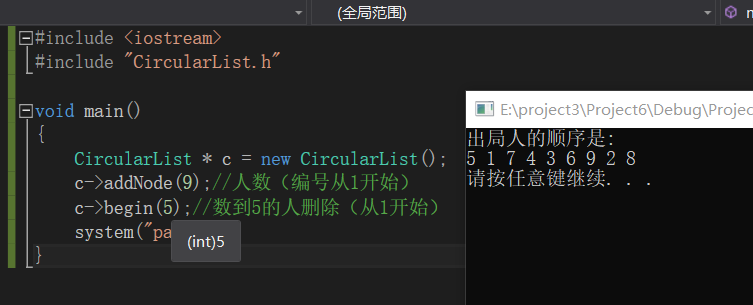
        输出：5 1 7 4 3 6 9 2 8

Node.h

#pragma once
class Node
{
public:
	int index;
	Node * prve;
	Node * next;
	Node(int index);
	~Node();
};

CircularList.h

#pragma once
#include "Node.h"
class CircularList
{
public:
	Node * root;//头节点
	Node * last;//尾节点
	int size=0;
	CircularList();
	~CircularList();

	void addNode(int num);//添加 num 个节点，编号为（0-num）
	Node * removeNode(Node * n);//删除节点
	void prinft();//打印节点

	int begin(int n);

};

Node.cpp

#include "Node.h"
#include <iostream>
Node::Node(int index)
{
	this->next = NULL;
	this->index = index;
}
Node::~Node()
{
}

CircularList.cpp

#include "CircularList.h"
#include "Node.h"
#include <iostream>
using namespace std;
//构造函数
CircularList::CircularList()
{
}
//析构函数
CircularList::~CircularList()
{
}
//添加节点
void CircularList::addNode(int num)
{
	root = new Node(1);
	last = root;
	for (int i=2;i<=num;i++)
	{
		Node * n = new Node(i);
		last->next = n;
		n->prve = last;
		last = n;
	}
	size = num;
}
//打印节点
void CircularList::prinft()
{
	Node * n = root;
	while (n != NULL)
	{
		cout << n->index << "\t";
		n = n->next;
	}
	cout << endl;
}
//删除节点
Node * CircularList::removeNode(Node * n)
{
	Node * node = n->next;
	n->prve->next = node;
	node->prve = n->prve;
	n->next = NULL;
	n->prve = NULL;
	cout << n->index<<" ";
	delete(n);
	size--;
	return node;
}

//找出最后一个节点
int CircularList::begin(int n)
{
	cout << "出局人的顺序是:" << endl;
	//形成循环链表
	if (last == NULL) 
	{
		return -1;
	}
	else 
	{
		last->next = root;
		root->prve = last;
	}
	int i = 1;//当前数字
	Node * node = root;//当前节点
	while (size>1)
	{
		if (i==n)
		{
			i = 1;
			node = removeNode(node);
		}
		else 
		{
			i++;
			node = node->next;
		}
	}
	cout << node->index << endl;
	return node->index;
}

Test.cpp

#include <iostream>
#include "CircularList.h"

void main()
{
	CircularList * c = new CircularList();
	c->addNode(9);//人数（编号从1开始）
	c->begin(5);//数到5的人删除（从1开始）
	system("pause");
}