leetcode第110题（简单）

原链接 https://leetcode-cn.com/problems/balanced-binary-tree/

题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例1

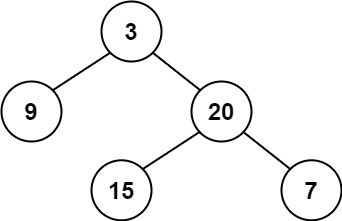
输入：root = [3,9,20,null,null,15,7] ，输出：true

示例2

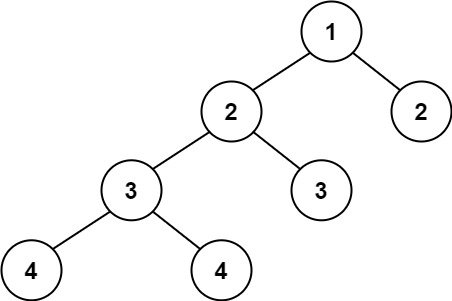
输入：root = [1,2,2,3,3,null,null,4,4]，输出：false

解题思路

递归，分治。

递归遍历二叉树所有节点，从叶子节点开始向上判断每个节点所在的子树，是否是平衡二叉树。直到树的根节点为平衡二叉树结束。

代码（java）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        dfs(root);
        return b;
    }
    boolean b=true;
    public int dfs(TreeNode root){
        if(root==null){
            return 0;
        }else{
            int left=dfs(root.left);
            if(!b){
                return 0;
            }
            int right=dfs(root.right);
            //System.out.println(Math.abs(left-right));
            if(Math.abs(left-right)<=1){
                return (left>right?left:right)+1;
            }else{
                b=false;
                return 0;
            }
        }
    }
}