再探a*搜索算法(启发式函数的影响)

前言

了解a*搜索算法的原理请参考：http://www.jiajiajia.club/official/weblog/32

a*搜索算法动态演示分析，及代码，请参考：http://photo.jiajiajia.club/item/a-star.html

Dijkstra算法与最佳优先搜索

在了解a*算法之前相信您已经对这两个算法有所了解

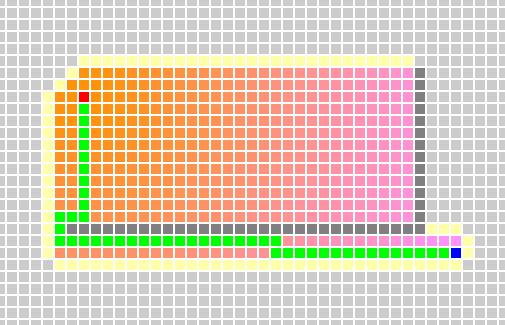
Dijkstra算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，优先从未遍历的节点集合中选取距离最近的那个节点遍历，然后再更新与该节点有关的接待你的距离，直到扩展到终点为止。条件是每条边的权值不能为负数。但是在某种情形中，和广度优先搜索一样，需要耗费更多的时间。如下图，红色为开始节点，蓝色为结束节点。

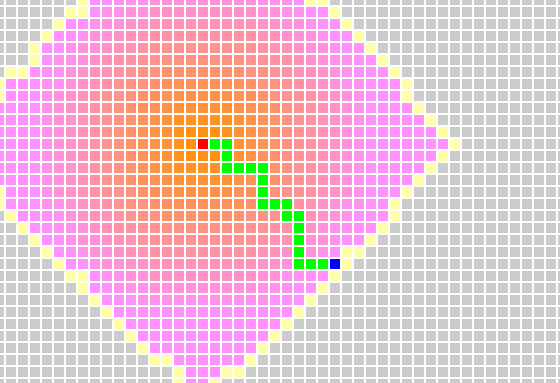
Dijkstra算法能够在复杂的环境中找到一条最短路径。如下图。

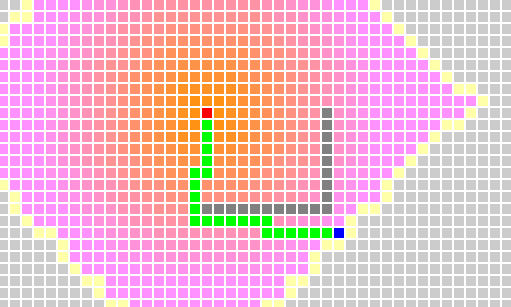
最佳优先搜索算法是一种启发式的搜索算法，它是对广度优先搜索算法的一种改进，它在广度优先搜索算法的基础上利用一个估价函数对将要遍历的节点进行估价（一般是从该节点到目标节点的距离），然后从将要遍历的集合中取出一个代价最小的节点遍历。这样的话它的速度就会提升很快。

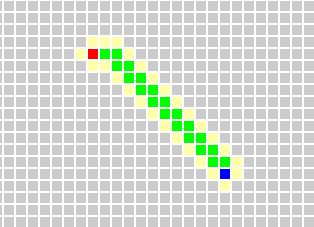
但是他的缺点是不能保证找到一条最短的路径。例如下面有障碍的情况，明显不是最短的路径。

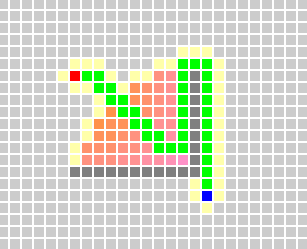
A*搜索算法

a*算法的实现在之前已经介绍过了,请参考原文：http://www.jiajiajia.club/official/weblog/32，在此就不解释实现原理了。

a* 算法结合了最佳优先搜索算法和 Dijkstra算法两者的优点：在进行启发式搜索提高算法效率的同时，还可以保证找到一条最优路径。因为a*算法同时把从开始节点走到当前节所消耗的代价g(n)（距离）和从当前节点到目标节点的预估代价h(n)（距离）同时作为选取下一节点的参考标准 f(n)。点也可以说启发式函数基本决定了a*搜索算法搜索的方向。

启发式函数：f(n)=g(n)+h(n)

g(n)为已知的从开始节点到当前节点经过的代价，h(n)为从当前节点到目标节点的预估代价。

那么选取下一节点的时候理应选取g(n)+h(n)和最小的节点作为下一将要遍历的节点。

所以f(n)函数的选取就成为了a*算法的核心。

启发式函数对a*搜索算法的影响

如果不考虑g(n)的情况或者g(n)要远小于h(n)，那么a*搜索算法就会逐渐趋向于最佳优先搜索。因为过分的把h(n)作为参考选择下一节点的标准，势必会以失去精准度为代价。在某种条件下，a*搜索算法不能找到一条最短路径。

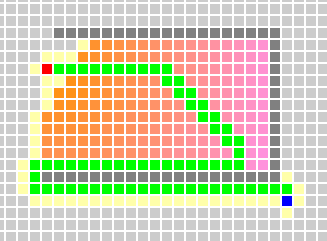
如果不考虑h(n)或g(n)远大于h(n)的时候，那么a*搜索算法会逐渐趋向于Dijkstra算法，他确实能找到一条最短路径，但是在某种条件下消耗的时间也是惊人的。

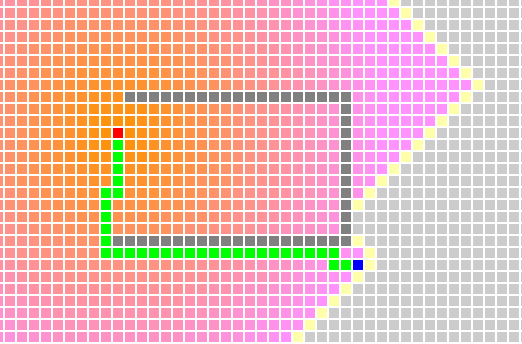
只有在均衡两者的关系的时候，才能满足和体现a*算法的特点，如下图。

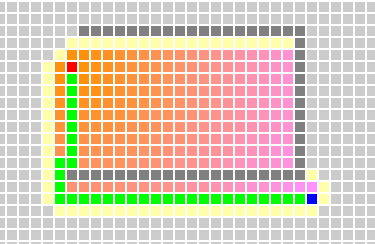
因为从开始节点到当前节点经过的距离即g(n)是根据特定情形而设定的，经过某节点时的时的距离经过Dijkstra算法的计算后也都是最近的。所以下一节点的选择几乎取决于h(n)的计算结果。

启发函数h(n)的选取

1.曼哈顿距离（城市街区距离）

D*(Math.abs(startX-endsX)+Math.abs(startY-endsY));

D为每走一步需要消耗的代价。

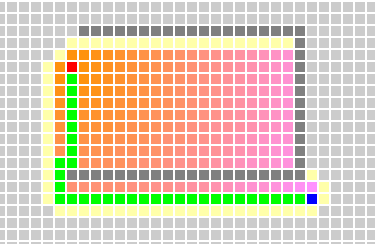
如果是只能四个方向走的时候，此时应该是较好的一种方案。

2.欧几里得距离

var a=Math.abs(startX-endsX);
var b=Math.abs(startY-endsY);
return D*Math.sqrt((a*a+b*b));

3.平方后的欧几里得距离

var a=Math.abs(startX-endsX);
var b=Math.abs(startY-endsY);
return D*(a*a+b*b);

4.对角线距离

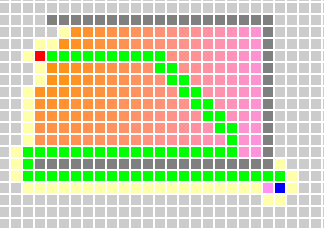
D*Math.max(Math.abs(startX-endsX),Math.abs(startY-endsY));

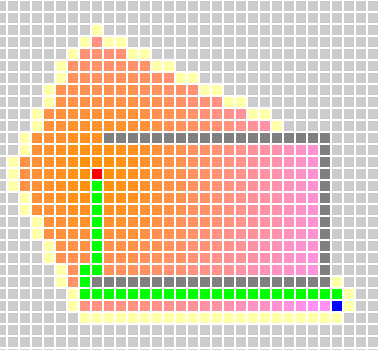
具体选取什么样的f(n)作为参考依据，还需要根据具体情况。