前言
之前的博客中提到了floyd最短路径算法,此算法的优点是,简单易懂,核心算法代码只有5行,但是缺点是时间复杂度o(n3),时间复杂度太高。而下面要介绍的Dijkstra算法虽然设计上略有复杂,但是时间复杂度确能降低到o(n2)。
百科
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
问题案例
还以之前提到的那个路径问题为例,连图也是复制过来的。
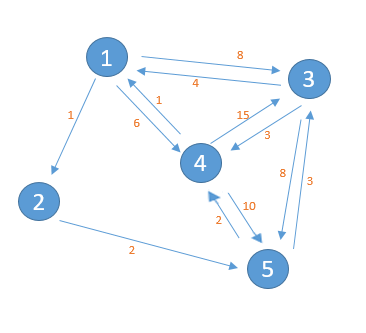
Dijkstra的算法思路
1.把所有的节点分为两个集合分别是S集合(探索过程中已知的最短路径的节点的集合),U集合(暂未探索的节点的结合,但是每个节点到达开始节点的距离是可知的,并且是随着探索的过程,到达开始节点的距离是可以不断变化的)。
2.每次探索从U集合中取出距离开始节点最近的那个节点。并将该节点加入S集合,然后更新与该节点相邻的U集合中的各个节点与开始节点的距离(
具体的更新过程是:
如果从开始节点到该节点的距离+从该节点到该节点的相邻节点的距离>开始节点到邻节点的距离,那么就更新开始节点到邻节点的距离
例:开始节点到该节点的距离为a,从该节点到该节点的相邻节点的距离为b, 从开始节点到该节点的相邻节点的距离为c,那么if(a+b>c){c=a+b}
)。
3.如果还没有探索到目标节点,那就一直执行探索过程2,直到达到目标节点结束。
呕心沥血的总结~
伪算法
S=[];
U=[];
While(不是目标节点){
K=从U集合中找出距离开始节点最近的节点。
将k节点加入S集合并标记已探索该节点K
//遍历U集合中所有的该节点的邻节点。
For(i=0;i<a;i++){
If(r[k][i]+r[start][k])<=r[start][i]){
//更新权值
r[start][i]=r[k][i]+r[start][k];
}
}
}
最后r[start][end]的值就是最短路径的距离。至于探索过程中经过的路径是什么~后边再说~
以上图为例,分解一下算法执行的过程
从节点1到节点4为例,从图中可以直接看出,从节点1直接到节点4距离为6,而从节点1经过节点2,再经过节点5到节点4的距离5。显然选择第二中方案更好。那么怎么做呢?
第一步先将开始节点1加入S集合
此时:S集合【1(0) 】 U集合【2(1) 3(8) 4(6) 5(∞) 】
第二步选择U集合中距离最小的节点2,加入S集合,并更新U集合中的距离。
此时:S集合【1(0) 2(1) 】 U集合【3(8) 4(6) 5(3) 】
第三步选择U集合中距离最小的节点5,加入S集合,并更新U集合中的距离。
此时:S集合【1(0) 2(1) 5(3) 】 U集合【3(6) 4(5) 】
第三步选择U集合中距离最小的节点4,加入S集合,并更新U集合中的距离。
此时:S集合【1(0) 2(1) 4(5) 5(3) 】 U集合【3(6) 】
这时已经遍历到目标节点4,所以从1节点到4的最短路径为5。
经过的路径为:[1, 2, 5, 4]
算法实现
算法中实现了求从开始节点到目标节点经过的路径,用一个数组parent保存经过该节点时的父节点。到达目标节点后可以用栈的结构反向推算出算法经过的路径。
package com.dzqc.yx;
import java.util.LinkedList;
/**
* Dijkstra算法
* @author jiajia
*/
public class Dijkstra {
/**
* m 代表正无穷(两个节点之间无法直接到达)
*/
public static final int m=Integer.MAX_VALUE>>3;
/**
* 邻接矩阵描述图
*/
public static final int r[][]=new int[][]{
{0,0,0,0,0,0},
{0,0,1,8,6,m},
{0,m,0,m,m,2},
{0,4,m,0,3,8},
{0,1,m,15,0,10},
{0,m,m,3,2,0}
};
/**
* 最短路径节点集合
*/
public static final int s[]=new int[r.length];
/**
* 父节点位置
*/
public static final int parent[]=new int[]{-1,-1,-1,-1,-1,-1};
public static void main(String[] args) {
int start=1;
int end=4;
dijkstra(start,end);
for(int i=1;i<parent.length;i++) {
System.out.print(i+":"+parent[i]+"\t");
}
System.out.println();
System.out.println("经过路径:"+role(start,end));
}
public static LinkedList<Integer> role(int start,int end) {
LinkedList<Integer> stack=new LinkedList<Integer>();
stack.add(end);
while(parent[end]!=-1) {
stack.addFirst(parent[end]);
end=parent[end];
}
stack.addFirst(start);
return stack;
}
/**
* 核心算法
* @param start
* @param end
*/
public static void dijkstra(int start,int end){
/**
* 第一个顶点放入s集合
*/
s[start]=1;
prinf(start);
int k = start;
while(s[end]!=1) {
/**
* 从u集合中选取一个权值最小的节点k
*/
int min=m;
for(int i=1;i<r.length;i++) {
if(s[i]!=1&&r[start][i]<min) {
min=r[start][i];
k=i;
}
}
s[k]=1;
System.out.println("选择的点为:"+k);
/**
* 修改节点的权值
*/
for(int i=1;i<r.length;i++) {
if(s[i]!=1&&(r[k][i]+r[start][k])<=r[start][i]) {
r[start][i]=r[k][i]+r[start][k];
parent[i]=k;
}
}
prinf(start);
}
System.out.println();
System.out.println("最短路:"+r[start][end]);
}
/**
* 打印S集合和U集合
* @param start
*/
public static void prinf(int start) {
System.out.println();
System.out.print("S集合【");
for(int i=1;i<r.length;i++) {
if(s[i]!=0) {
System.out.print(i+"("+r[start][i]+") ");
}
}
System.out.print("】\nU集合【");
for(int i=1;i<r.length;i++) {
if(s[i]!=1) {
System.out.print(i+"("+r[start][i]+") ");
}
}
System.out.print("】");
}
}

