1.PMT
KMP算法的核心,是一个被称为部分匹配表(Partial Match Table)的数组。我觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后,仍然搞不懂PMT中的值代表了什么意思。先来解释一下这个数据到底是什么。对于字符串“abababca”,它的PMT如下表所示:
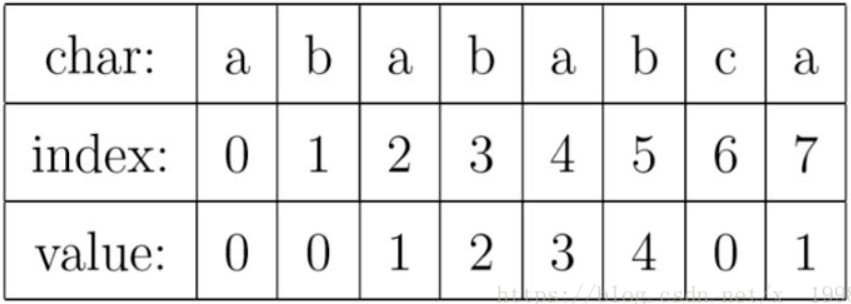
就像例子中所示的,如果待匹配的模式字符串有8个字符,那么PMT就会有8个值。
解释一下字符串的前缀和后缀。如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。要注意的是,字符串本身并不是自己的后缀。
有了这个定义,就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如,对于”aba”,它的前缀集合为{”a”, ”ab”},后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”},那么长度最长的元素就是字符串”a”了,长 度为1,所以对于”aba”而言,它在PMT表中对应的值就是1。再比如,对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。
2.PMT的实现
package problem;
public class PMT {
public static void main(String[] args) {
int []a=pmt("ababaaababa");
for(int b:a){
System.out.print(b+" ");
}
}
//PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度
public static int[] pmt(String pattern){
int[] pmt = new int[pattern.length()];
int ml = 0;
for (int i = 1; i < pattern.length(); i++) {
while (ml > 0 && pattern.charAt(ml) != pattern.charAt(i)) {
ml = pmt[ml - 1];
}
if (pattern.charAt(i) == pattern.charAt(ml)) {
ml++;
}
pmt[i] = ml;
}
return pmt;
}
}
3.匹配方法实现
/*
* kmp
*/
public static List<Integer> kmp(String text, String pattern){
List<Integer> positions = new ArrayList<>();
int[] pmt = pmt(pattern);
int count = 0;//count指向模式串
for (int i = 0,k=text.length(); i <k ; i++) {//i指向主串
while (count > 0 && pattern.charAt(count) != text.charAt(i)) {//失配
count = pmt[count - 1];//模式串指向前缀最有可能匹配的位置
}
if (pattern.charAt(count) == text.charAt(i)) {//匹配,指针向前走
count++;
}
if (count == pattern.length()) {//匹配成功
positions.add(i - pattern.length() + 1);
count = pmt[count - 1];//寻找下一匹配位置
}
}
return positions;
}
4.代码实现:
package KMP;
import java.util.ArrayList;
import java.util.List;
public class PMT {
public static void main(String[] args) {
List<Integer> b=kmp("acbabac","ac");
for(Integer a:b){
System.out.println(a);
}
}
//PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度
//前缀函数(失配函数)
public static int[] pmt(String pattern){
int[] pmt = new int[pattern.length()];
int maxLength = 0;
for (int i = 1; i < pattern.length(); i++) {
while (maxLength > 0 && pattern.charAt(maxLength) != pattern.charAt(i)) {
maxLength = pmt[maxLength - 1];
}
if (pattern.charAt(i) == pattern.charAt(maxLength)) {
maxLength++;
}
pmt[i] = maxLength;
}
return pmt;
}
/*
* kmp
*/
public static List<Integer> kmp(String text, String pattern){
List<Integer> positions = new ArrayList<>();
int[] pmt = pmt(pattern);
int count = 0;//count指向模式串
for (int i = 0,k=text.length(); i <k ; i++) {//i指向主串
while (count > 0 && pattern.charAt(count) != text.charAt(i)) {//失配
count = pmt[count - 1];//模式串指向前缀最有可能匹配的位置
}
if (pattern.charAt(count) == text.charAt(i)) {//匹配,指针向前走
count++;
}
if (count == pattern.length()) {//匹配成功
positions.add(i - pattern.length() + 1);
count = pmt[count - 1];//寻找下一匹配位置
}
}
return positions;
}
}


