[数据结构与算法]
一、简介
wiki上关于并查集的简介
在计算机科学中,并查集是一种树型的数据结构,用于处理一些不交集(Disjoint Sets)的合并及查询问题。有一个联合-查找算法(union-find algorithm)定义了两个用于此数据结构的操作:
- Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合。
并查集主要用于解决动态连通性问题
我们用一个代表来标识一个不交集. 通常我们不关心哪个成员作为代表, 但是对于属于同一个集合的两个变量, 查询应该得到相同的代表。
举个栗子,假如有一个大型的计算机网络, 其中有很多台计算机, 如果计算机a与计算机b连通, b与c连通, 那么a与c连通. 对于网络中的两台计算机p, q我们可能有这些操作: 判断p, q是否连通find(p) == find(q);在p, q之间建立一条路线使两者连通union(p, q)
通过上面的例子不难看出连通是一种等价关系, 它有以下性质:
- 自反性: p与p是连通的
- 对称性: p与q连通, 则q与p连通
- 传递性: p与q连通且q与r连通, 则p与r连通
二、算法实现
首先我们用一个数组记录所有元素, 对于set[i] == k , i表示i个元素, k表示元素所属的集合, 通常可以指向或者间接指向集合的代表来表示属于这个集合. 当set[i] == i是表明i是一个根节点。
set[i] ==k可以理解为i, k之间有一条连通的路线, 被称为链接。
初始化
让所有元素指向自己, 表示属于不同的集合, 此时集合中每个元素都是一个根节点
private int[] parent;
public void init(int n) {
parent = new int[n];
for (int i = 0; i < n; i++)
parent[i] = i;
}
Find
从x向上查找, 直到找到元素的根节点set[i] == i, 此根节点就表示这个集合。
public int find(int x) {
if (parent[x] != x) {
find(parent[x]);
}
return parent[x];
}
Union
把两个不同的点连起来, 对于x ,y两个点来说, 相当与把x, y所在集合合并(传递性), 即x, y所在集合所以元素都连通. 所以我们可以找到两个集合的代表(根节点), 然后把代表合并即可。
public void union(int x, int y) {
// 分别查询x、y所在集合的代表
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
// 如果存在同一个集合中,则返回
return;
}
// 选取rootY作为新集合的代表,把x所在集合合并到y集合
parent[rootX] = rootY;
}
我们在选取谁合并到谁时是随便选取的, 实际上合理的选取能够很好地优化算法。
三、图示
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
1 |
9 |
2 |
5 |
9 |
1 |
9 |
7 |
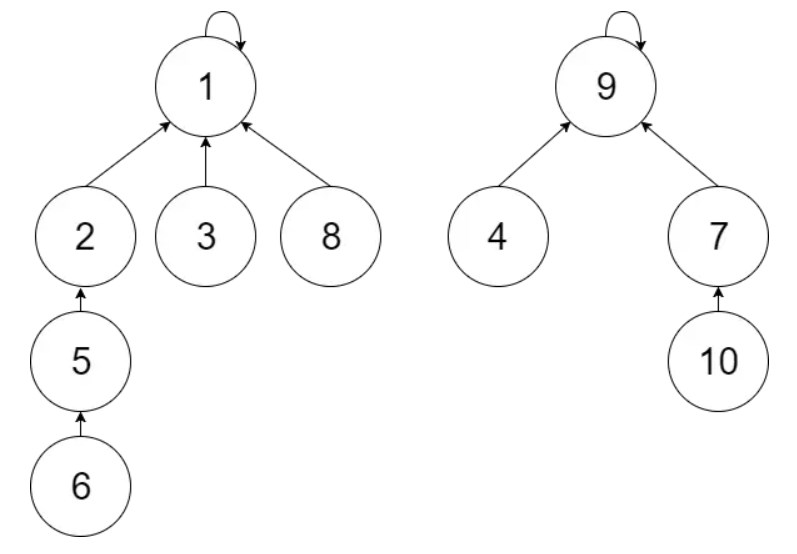
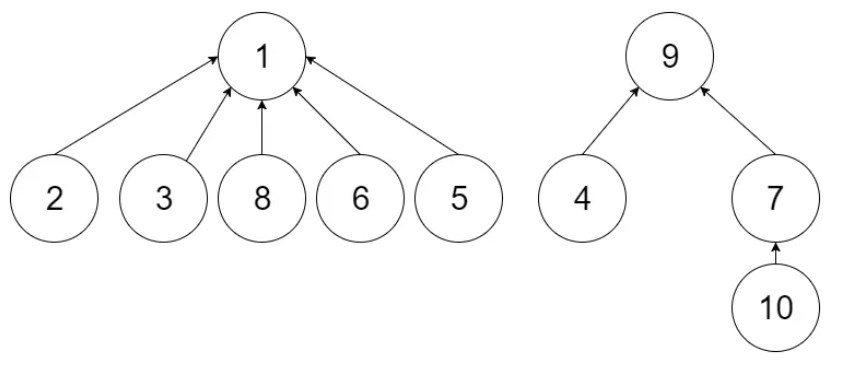
find(6)即为parent[parent[parent[parent[6]]]] == 1
find(7)即为parent[parent[7]] == 9
![]()
union(6, 7)
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 9 |
1 |
1 |
9 |
2 |
5 |
9 |
1 |
9 |
7 |
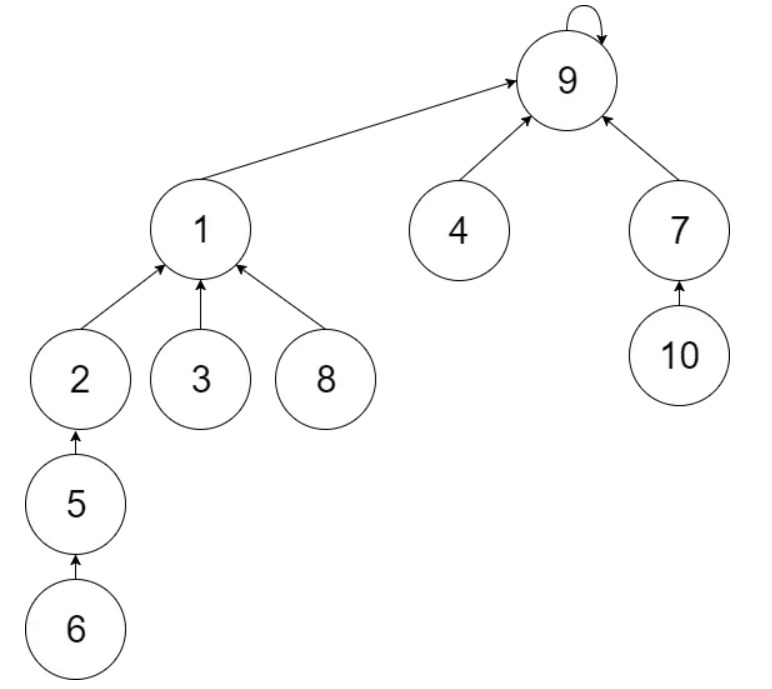
则rootX = 1, rootY = 9, 即parent[1] = 9
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 9 |
1 |
1 |
9 |
2 |
5 |
9 |
1 |
9 |
7 |
合并完如图:
![]()
四、算法优化
上面提到合并是随意选取的, 那么怎么选取可以优化算法呢. 考虑find算法的过程, 从低向上查找代表, 那么树的高度就决定了find的快慢. 所以我们合并时可以考虑把比较矮的树合并到比较高的树上, 这样可以有效降低树的高度, 从而达到优化算法的目的
启发式合并
定义一个数组rank,记录每个节点的树高度,合并时,让较低的树合并到较高的树上,以达到有效降低树高的目的。
private int[] rank;//记录树的高度
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
// 比较树高,让较低的树合并到较高的树上
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
}
图示:
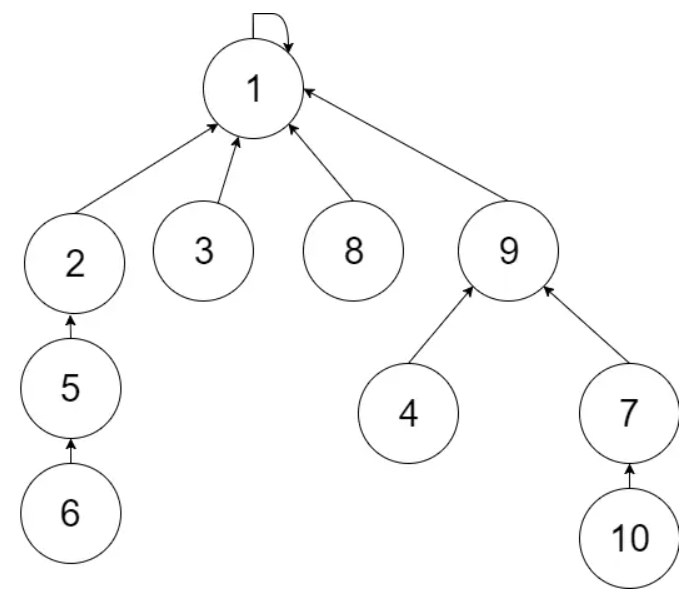
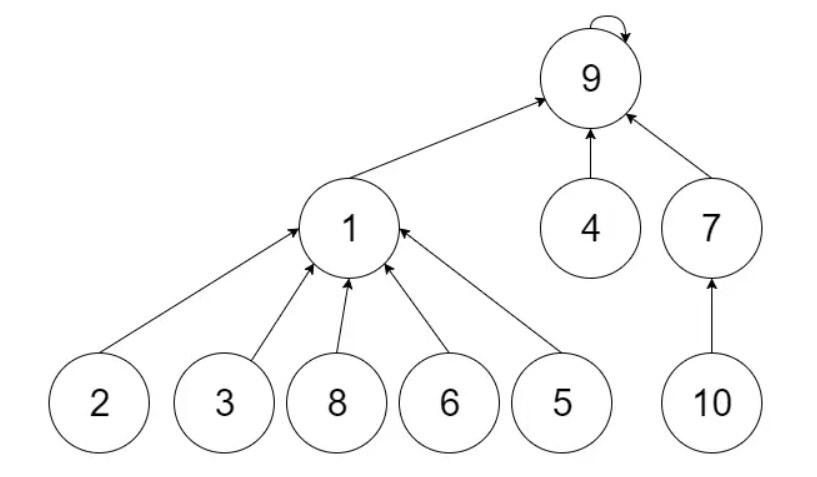
union(6, 7), 因为6所在树比7所在树高且大, 所以此时parent[9] = 1
可以看到相比没有优化的算法, 这种合并方式有效地降低了树高
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
1 |
9 |
2 |
5 |
9 |
1 |
1 |
7 |
![]()
路径压缩
既然把树高降低能优化算法, 那么我们能在find中降低树高吗?
我们可以在find中把查找路径上遇到的所有节点都直接链接到根节点, 从而实现路径压缩, 把树高降低。
代码十分简单, 甚至不比上面的复杂. 时间复杂度非常接近但是没有达到1
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
路径压缩图示
![]()
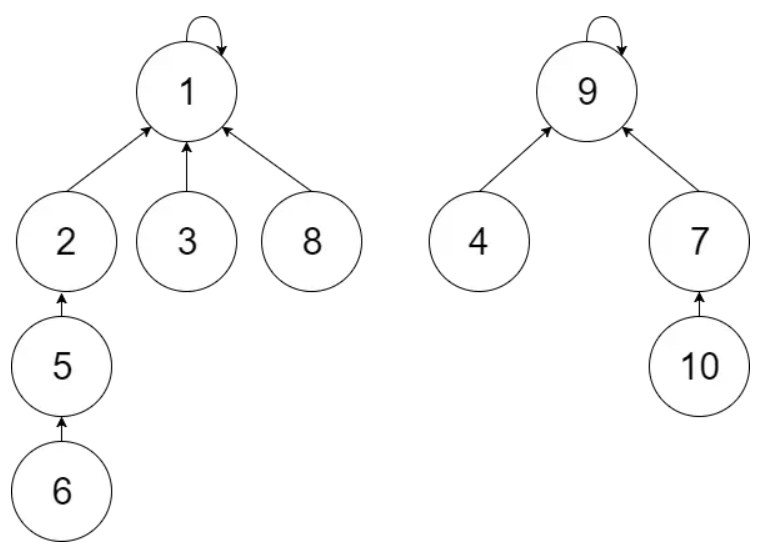
合并6、7两棵树union(6, 7)
先会调用find(6), find(7), 查找路径上的所以元素都会直接和根节点链接。
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 1 |
1 |
1 |
9 |
1 |
1 |
9 |
1 |
9 |
7 |
![]()
之后 parent[1] = 9
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 9 |
1 |
1 |
9 |
1 |
1 |
9 |
1 |
9 |
7 |
![]()
五、小结
- 路径压缩加上启发式合并就是并查集算法的最优解.
- 一般来说用路径压缩算法就足够了, 可以不再用启发式合并或者加权