熄灯问题

1.问题描述

有一个有按钮组成的矩阵，其中每行有6个按钮，共5行。

每个按钮的位置上有一盏灯。

当按下一个按钮后，该按钮以及周围位置（上下左右）的灯都会改变一次。即（原来亮的变暗，原来暗的变亮）

对矩阵中的每一盏灯设置一个初始状态。

请你写一个程序，确定需要按下那些按钮，插好使得所有的灯都被熄灭。

例图1：

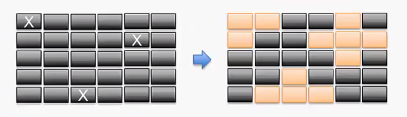
例图2：

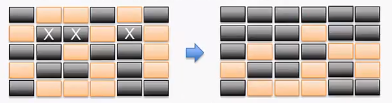
叉号代表按下的按钮

输入：

第一行是一个正整数n表示需要解决的案例数。

每一个案例由5行组成，每一行包括6个数字

这些数字以空格隔开，可以是0或1，0表示初始状态时熄灭的，1表示初始状态是点亮的。

输出：

对于每个案例都先输出一行“case#m”,m是案例序号

接着按照该案例的输入格式输出5行，

1表示需要把对应的按钮按下，

0表示不需要按对应的按钮。

2.算法实现（c语言实现）：

#include <stdio.h>
int puzzle[6][8],press[6][8];
int guess(){
       int c,r;
       for(r=1;r<5;r++){
              for(c=1;c<7;c++){
                     press[r+1][c]=(puzzle[r][c]+press[r][c]+
                            press[r-1][c]+press[r][c-1]+press[r][c+1])%2;
              }
       }
       for(c=1;c<7;c++){
              if((press[5][c-1]+press[5][c]+press[5][c+1]+
                     press[4][c])%2!=puzzle[5][c]){
                     return 0;
              }
       }
       return 1;
}
 
void enumerate(){
       int c;
       for(c=0;c<7;c++){
              press[1][c]=0;
       }
       while(guess()==0){
              press[1][1]++;
              c=1;
              while(press[1][c]>1){
                     press[1][c]=0;
                     c++;
                     press[1][c]++;
              }
       }
       return;
}
 
int main(){
       int cases,i,r,c;
       scanf("%d",&cases);
       for(r=0;r<6;r++){
              press[r][0]=press[r][7]=0;
       }
       for(c=1;c<7;c++){
              press[0][c]=0;
       }
       for(i=0;i<cases;i++){
              for(r=1;r<6;r++){
                     for(c=1;c<7;c++){
                            scanf("%d",&puzzle[r][c]);
                     }
              }
              enumerate();
              printf("case%d\n",i+1);
              for(r=1;r<6;r++){
                     for(c=1;c<7;c++){
                            printf("%d",press[r][c]);
                     }
                     printf("\n");
              }
       }
       return 0;
}

3.算法思路：

以第一行作为一个局部；

当第一行的按钮全部作用完以后，第一行可能还会存在部分按钮是亮的

那么要想熄灭第一行第i列的灯，必须按下第二行第i列的灯，类似的，要想熄灭第n行第i列的灯，就需要按下第n+1行，第i列的灯，直到第5行。

其含义是，要想让第一行的灯全部熄灭，那么后面的所有行的灯按下的情况就已经确定。如果作用完最后一行，发现，最后一行的灯也全部熄灭，那么按下的过程就是一个解。