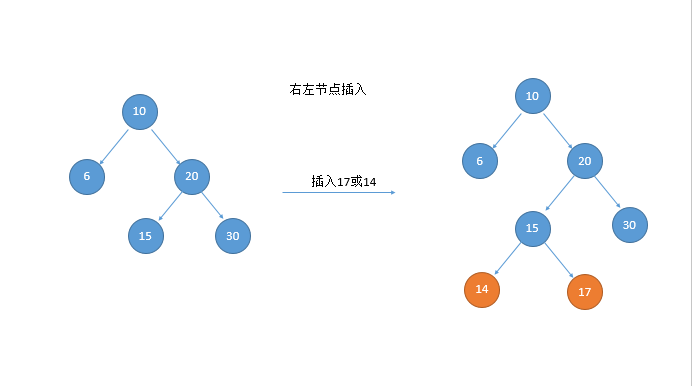
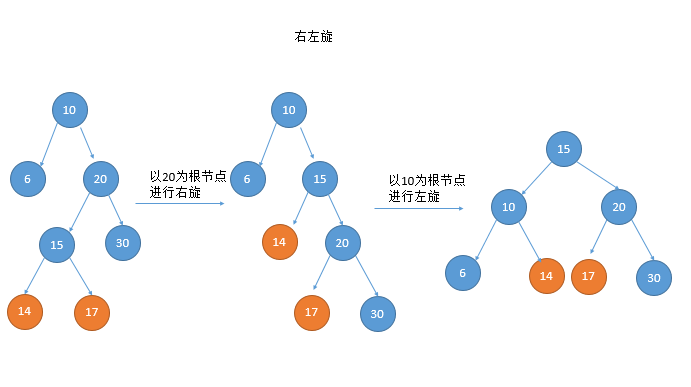
avl树：AVL树本质上是一颗二叉查找树

1.avl树的性质

        左子树和右子树的高度之差的绝对值不超过1

        树中的每个左子树和右子树都是AVL树

        每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1之一

2.avl树的操作

        AVL树的操作基本和二叉查找树一样，这里我们关注的是两个变化很大的操作：插入和删除！

        AVL树不仅是一颗二叉查找树，它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理，在删除的时候也有可能会破坏树的平衡性，所以我们要做一些特殊的处理，包括：单旋转和双旋转！

/**
	 * 返回较大的值
	 * @param l
	 * @param r
	 * @return
	 */
	public int max(int l, int r){
	    return (l > r ? l : r);
	}
	/**
	 * 获取树高度
	 * @param n
	 * @return
	 */
	public int hight(Node<Integer> n) {
	    if(n==null)
	        return -1;
	    else
	        return n.high;
	}

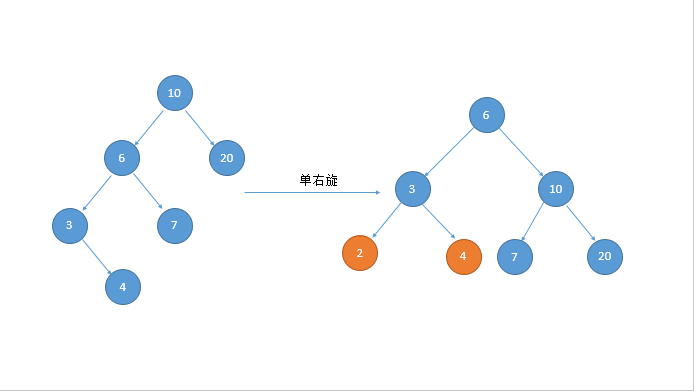
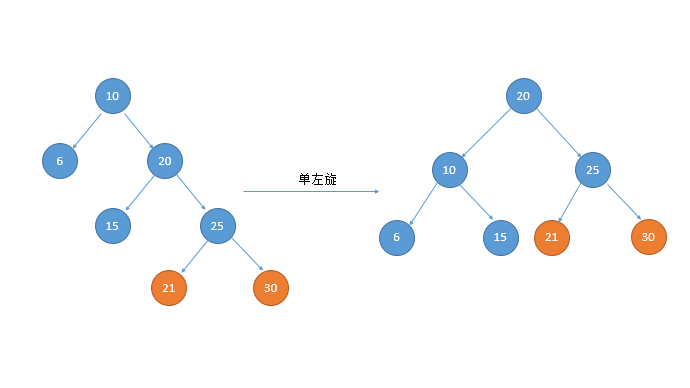
3.单旋转：

单旋的第一种情况：右旋

	/**
	 * 整个树是右旋的单旋转
	 * @param head
	 * @return
	 */
	public Node<Integer> singleRotateRight(Node<Integer> head){
		Node<Integer> tmp = head.left;
	    head.left = tmp.right;
	    tmp.right = head; //旋转后深度随之变化，需要修改深度
	    head.high = max(hight(head.left), hight(head.right)) + 1;
	    tmp.high = max(hight(tmp.left), hight(tmp.right)) + 1;
	    return tmp;//返回新的子树根节点
	}

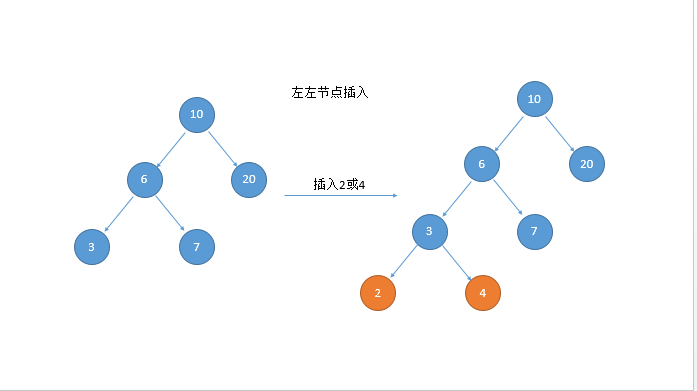
单旋的第二种情况：左旋

	/**
	 * 整个树是左旋的单旋转
	 * @param head
	 * @return
	 */
	public Node<Integer> singleRotateLeft(Node<Integer> head){
		Node<Integer> tmp = head.right;
	    head.right = tmp.left;
	    tmp.left = head;
	    head.high = max(hight(head.left), hight(head.right)) + 1;
	    tmp.high = max(hight(tmp.left), hight(tmp.right)) + 1;
	    return tmp;
	}

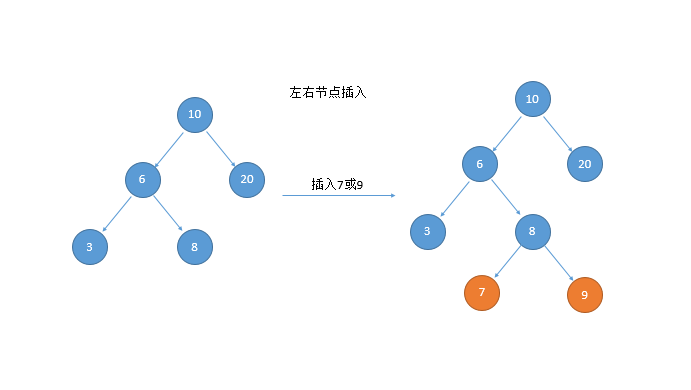
4.双旋转：

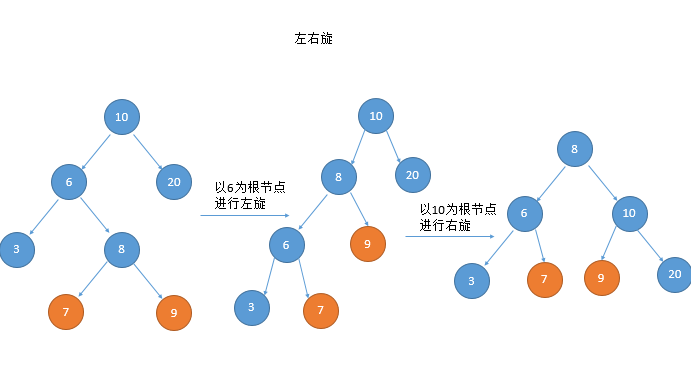
双旋的第一种情况：左右(先左后右)旋

	/**
	 * 整个树是右旋的双旋转
	 * @param head
	 * @return
	 */
	public Node<Integer> doubleRotateRight(Node<Integer> head){
	    head.left = singleRotateLeft(head.left);
	    return singleRotateRight(head);//再将整个树左旋
	}

双旋的第二种情况：右左(先右后左)旋

	/**
	 * 整个树是左旋的双旋转
	 * @param head
	 * @return
	 */
	public Node<Integer> doubleRotateLeft(Node<Integer> head){
	    head.right = singleRotateRight(head.right);
	    return singleRotateLeft(head);//再将整个树右旋
	}