1.问题描述：

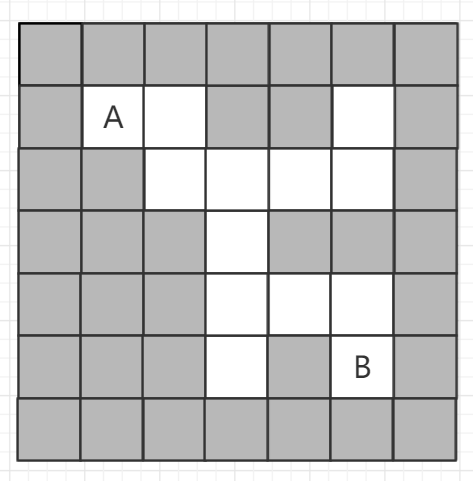
问题：上面有一个迷宫，灰色部分代表不能通过，白色部分代表可以通过，现在从a点出发，能否找到一条路径到达b点，如果能，输出此路径。

下面采用试探法求解，采用栈结构保存每一步的内容（包括坐标和方向），每前进一步都进行四个方向的试探，如果该方向可以走，就先记录下上一步走过的路径坐标，放进栈中保存，如果四个方向都无法通行，就从栈中取出上一次的路径坐标，换个方向继续试探，直到求解问题。

2.基本算法如下：

        (1)在(1,1)进入迷宫,并向正东(v=1)方向试探。

        (2)监测下一方位(g,h)。若(g,h)=(m,n)且 maze[m,n]=0,则到达出口,输出走过的路径:程序结束。

        (3)若(g,h)≠(m,n),但(g,h)方位能走通且第一次经过则记下这一步,并从(g,h)出发,再向东试探下一步否则仍在(i,j)方位换一个方向试探。

        (4)若(,j方位周围4个方位阻塞或已经过,则需退一步并换一个方位试探。若(i,j)=(1,1)则到达入口,说明迷宫走不通。

3.代码演示：

package problem;
public class State {
	public int i;//当前位置横坐标
	public int j;//当前位置纵坐标
	public int getI() {
		return i;
	}
	public State(int i, int j, int v) {
		super();
		this.i = i;
		this.j = j;
		this.v = v;
	}
	public void setI(int i) {
		this.i = i;
	}
	public int getJ() {
		return j;
	}
	public void setJ(int j) {
		this.j = j;
	}
	public int getV() {
		return v;
	}
	public void setV(int v) {
		this.v = v;
	}
	public int v;//当前方向
}

package problem;
import java.util.Stack;
/**
 * 栈的应用-迷宫问题
 * @author LENOVO
 *
 */
public class Maze {
	private static int maze[][];//代表迷宫矩阵
	private static int mark[][];//标记该坐标是否已经走过
	private static int move[][];//方向上的增量（包括四个方向）
	
	public static void main(String[] args) {
		move= new int[][] {{0,0},{0,1},{1,0},{0,-1},{-1,0}};
		mark=new int[7][7];
		maze=new int[][]{{1,1,1,1,1,1,1},
						 {1,0,0,1,1,0,1},
						 {1,1,0,0,0,0,1},
						 {1,1,1,0,1,1,1},
						 {1,1,1,0,0,0,1},
						 {1,1,1,0,1,0,1},
						 {1,1,1,1,1,1,1}};
		maze();
	}
	/**
	 * 试探
	 */
	public static void maze() {
		//栈，用于保存走每一步的信息，包括每一步的坐标和方向
		Stack<State> stack=new Stack<State>();
		State s=new State(1, 1, 1);
		mark[1][1]=1;
		do {
			int g=s.i+move[s.v][0],h=s.j+move[s.v][1];
			if((g==5&&h==5)&&maze[5][5]==0) {//找到出口
				System.out.println("找到出口");
				Stack<State> s_=new Stack<State>();
				stack.add(s);
				while(!stack.isEmpty()) {
					s_.add(stack.pop());
				}
				while(!s_.isEmpty()) {
					State l=s_.pop();
					System.out.println("坐标："+l.getI()+"-"+l.getJ());
				}
				return;
			}
			if(maze[g][h]==0&&mark[g][h]==0) {//可以向前走
				mark[g][h]=1;
				stack.add(s);
				s=new State(g,h,1);
			}else if(s.v<4) {//换个方向试探
				s.v++;
			}else {//无路可走，返回一步，从栈中取出记录的数据
				while(s.v>=4&&!stack.isEmpty()) {
					s=stack.pop();
					s.v++;
				}
			}
		}while(!stack.isEmpty()&&s.v<=4);//栈不为空，并且还有方向可以试探，则继续试探
		System.out.println("没有找到出口");
	}
}

move二维数组  的含义是：

横坐标代表方向：1-向右，2-向下，3-向左，4-向上，0-无意义

纵坐标代表位置坐标：0-横坐标，1-纵坐标

值代表该位置上的增量：比如：

    move[1,0]=0代表：横坐标向左不变

    move[1,1]=1代表：纵坐标向右走1个单位