[数据结构与算法]

• 一、什么是最小生成树？
• 二、Kruskal算法
• 三、Prim算法

一、什么是最小生成树？

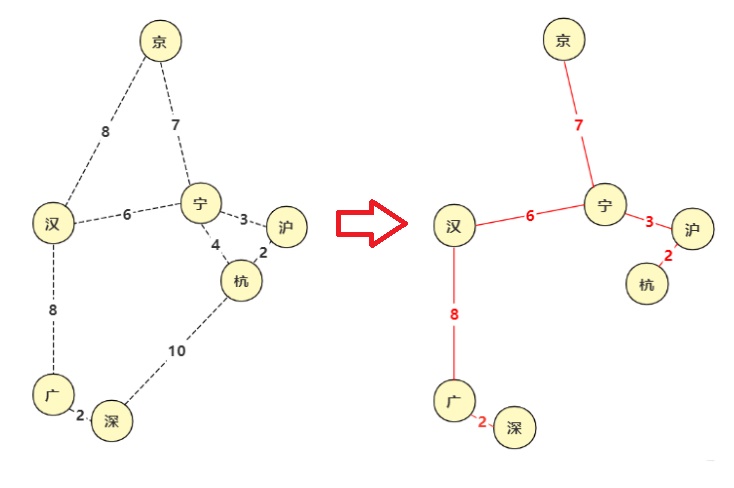
  在给定一张无向图，如果在它的子图中，任意两个顶点都是互相连通，并且是一个树结构，那么这棵树叫做生成树。当连接顶点之间的图有权重时，权重之和最小的树结构为最小生成树！

  在实际中，这种算法的应用非常广泛，比如我们需要在n个城市铺设电缆，则需要n-1条通信线路，那么我们如何铺设可以使得电缆最短呢？最小生成树就是为了解决这个问题而诞生的！

二、Kruskal算法

算法思想：先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

  该算法用到了并查集，用于操作树的查找和合并，如果不了解并查集这种数据结构应该先了解它的用法，才能更好的理解Kruskal算法。

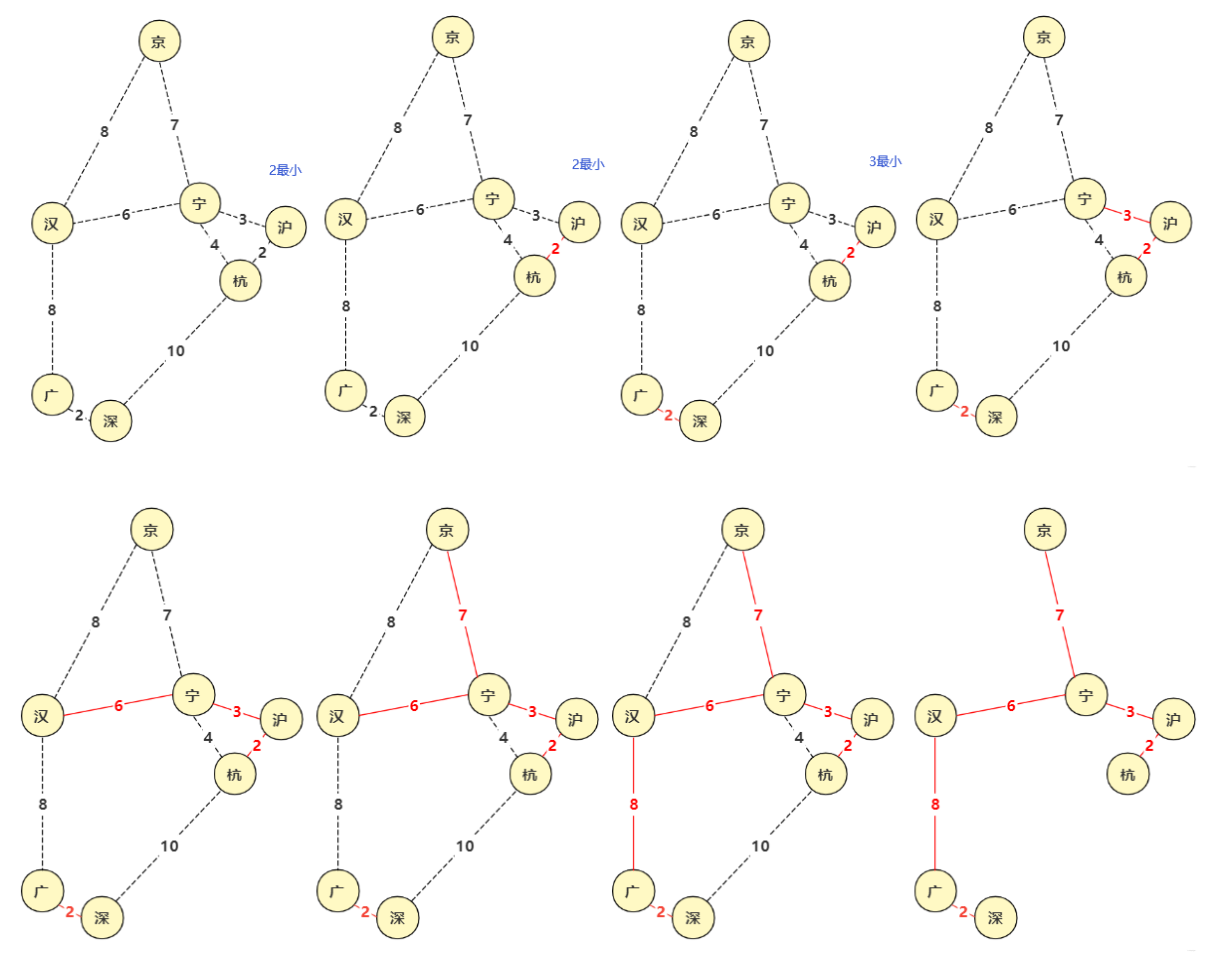
算法步骤：

• 1.将图中所有边对象(边长、两端点)依次加入集合(优先队列)queue中。初始所有节点为根节点。
• 2.取出集合(优先队列)queue最小边，判断边的两节点是否联通。
• 3.如果联通说明两个点已经有其它边将两点联通了，跳过，如果不连通，则使用union（并查集合并）将两个根节点合并，标记这条边被使用(可以储存或者计算数值)。
• 4.重复2，3操作直到集合（优先队列）queue为空。此时被选择的边构成最小生成树。

代码案例

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
/**
 * @author : Jiajiajia
 * @createDate : 2023/4/20 15:08
 * @description : 最小生成树（Kruskal算法）
 */
public class Kruskal {
    static int max = Integer.MAX_VALUE;
    static String[] node = new String[]{"北京","武汉","南京","上海","杭州","广州","深圳"};
    static int[] nodeParent = new int[node.length];
    static int[] rank=new int[node.length];//记录树的高度
    static int map[][]= {
            { max, 8, 7, max, max, max, max }, //北京和武汉南京联通
            { 8, max,6, max,9, 8,max }, //武汉——北京、南京、杭州、广州
            { 7, 6, max, 3,4, max,max }, //南京——北京、武汉、上海、杭州
            { max, max,3, max,2, max,max }, //上海——南京、杭州
            { max, 9,4, 2,max, max,10 }, //杭州——武汉、南京、上海、深圳
            { max, 8,max, max,max, max,2 }, //广州——武汉、深圳
            { max, max,max, max,10,2,max }//深圳——杭州、广州
    };
    // 优先队列
    static Queue<Line> queue=new PriorityQueue<Line>(new Comparator<Line>() {
        @Override
        public int compare(Line o1, Line o2) {
            // TODO Auto-generated method stub
            return o1.value-o2.value;
        }
    });
    public static void main(String[] args) {
        for (int i=0;i<node.length;i++){
            for (int j=i;j<node.length;j++){
                if(i!=j && map[i][j] != max){
                    queue.add(new Line(map[i][j],new Node(i),new Node(j)));
                }
            }
        }
        init(); //初始化并查集
        Line line = null;
        int minLength = 0;
        while ((line = queue.poll()) != null){
            // 从优先队列中获取一个最短的路径，判断改路径上的两个点，是否在同一棵树上，
            // 如果不在同一棵树上，则将两个点合并到同一棵树上
            final int x = find(line.x.value);
            final int y = find(line.y.value);
            if(x != y){
                union(x,y);
                minLength += line.value;
                System.out.println(node[line.x.value]+" "+node[line.y.value]+" 联通");
            }
        }
        System.out.println("最短路径："+minLength);
    }
    // 初始化并查集
    static void init(){
        for(int i = 0 ; i < nodeParent.length ; i++){
            nodeParent[i] = i;
            rank[i] = 0;
        }
    }
    // 查询代表
    static int find(int x){
        if (nodeParent[x] != x) {
            nodeParent[x] = find(nodeParent[x]);
        }
        return nodeParent[x];
    }
    // 合并树
    static void union(int x,int y){
        int rootX = find(x);
        int rootY = find(y);
        if (rootX == rootY) {
            return;
        }
        // 比较树高，让较低的树合并到较高的树上
        if (rank[rootX] < rank[rootY]) {
            nodeParent[rootX] = rootY;
        } else if (rank[rootX] > rank[rootY]) {
            nodeParent[rootY] = rootX;
        } else {
            nodeParent[rootY] = rootX;
            rank[rootX]++;
        }
    }
    // 边
    static class Line{
        private int value;
        private Node x;
        private Node y;
        public Line(int value,Node x,Node y){
            this.value = value;
            this.x = x;
            this.y = y;
        }
    }
    // 点
    static class Node{
        public Node(int value){
            this.value = value;
        }
        private int value;
    }
}

三、Prim算法

  除了Kruskal算法以外，普里姆算法（Prim算法）也是常用的最小生成树算法。虽然在效率上差不多。但是贪心的方式和Kruskal完全不同。

  prim算法的核心信仰是：从已知扩散寻找最小。它的实现方式和Dijkstra算法相似但稍微有所区别，Dijkstra是求单源最短路径，而每计算一个点需要对这个点重新更新距离，而prim不用更新距离。直接找已知点的邻边最小加入即可！prim和kruskal算法都是从边入手处理。

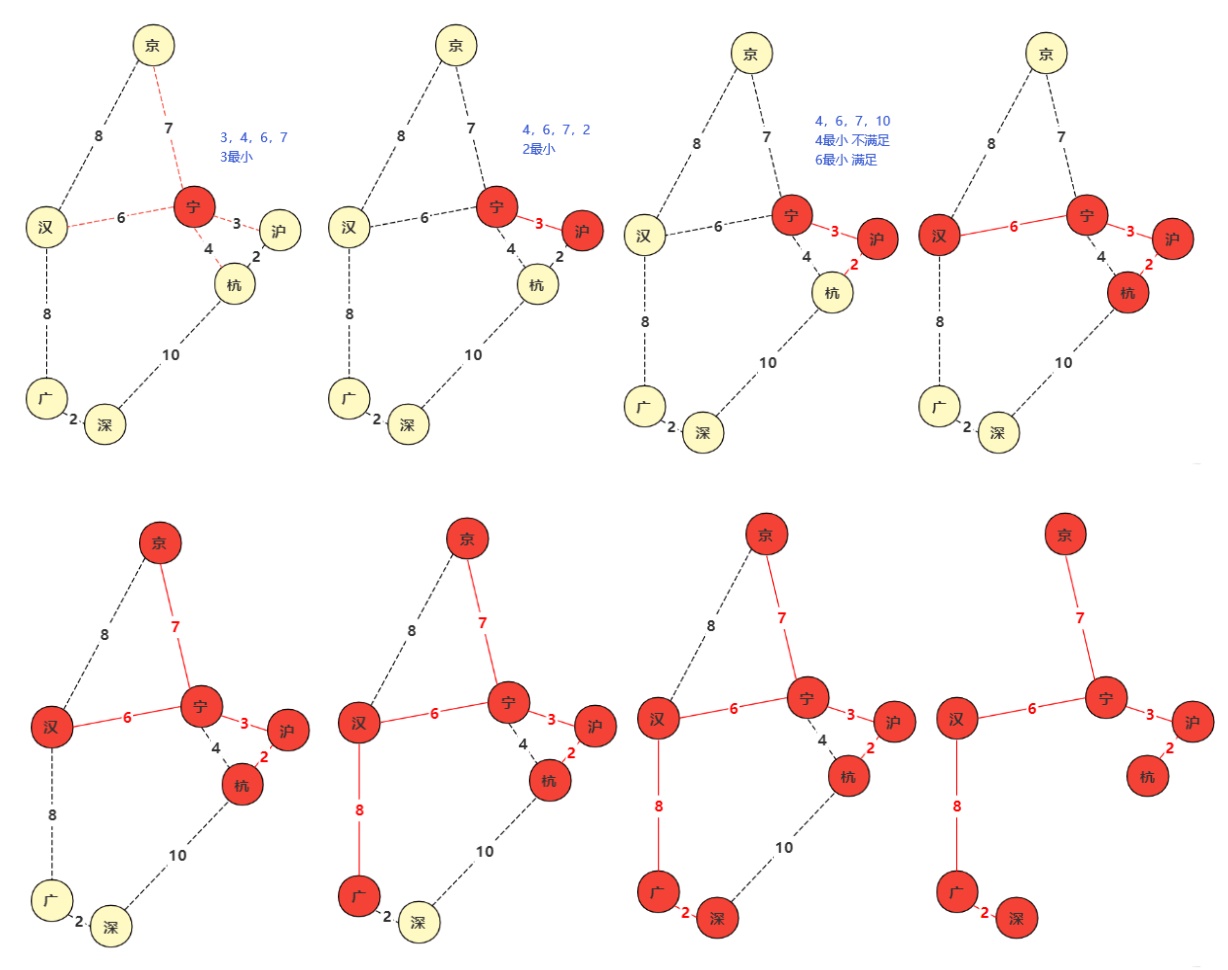
算法步骤：

• 1.寻找图中任意点，以它为起点，它的所有边V加入集合(优先队列)queue,设置一个boolean数组bool[]标记该位置(边有两个点，每次加入没有被标记那个点的所有边)。
• 2.从集合queue找到距离最小的那个边v1并 判断边是否存在未被标记的一点p ，如果p不存在说明已经确定过那么跳过当前边处理，如果未被标(访问)记那么标记该点p,并且与p相连的未知点(未被标记)构成的边加入集合q1， 边v1(可以进行计算距离之类，该边构成最小生成树) .
• 3.重复1，2直到q1为空，构成最小生成树 ！

  因为prim从开始到结束一直是一个整体在扩散，所以不需要考虑两棵树合并的问题，在这一点实现上稍微方便了一点。

代码案例

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
/**
 * @author : Jiajiajia
 * @createDate : 2023/4/20 15:08
 * @description : 最小生成树（Prim算法）
 */
public class Prim {
    static int max = Integer.MAX_VALUE;
    static String[] node = new String[]{"北京","武汉","南京","上海","杭州","广州","深圳"};
    static boolean[] tag = new boolean[node.length];
    static int map[][]= {
            { max, 8, 7, max, max, max, max }, //北京和武汉南京联通
            { 8, max,6, max,9, 8,max }, //武汉——北京、南京、杭州、广州
            { 7, 6, max, 3,4, max,max }, //南京——北京、武汉、上海、杭州
            { max, max,3, max,2, max,max }, //上海——南京、杭州
            { max, 9,4, 2,max, max,10 }, //杭州——武汉、南京、上海、深圳
            { max, 8,max, max,max, max,2 }, //广州——武汉、深圳
            { max, max,max, max,10,2,max }//深圳——杭州、广州
    };
    // 优先队列
    static Queue<Line> queue=new PriorityQueue<Line>(new Comparator<Line>() {
        @Override
        public int compare(Line o1, Line o2) {
            // TODO Auto-generated method stub
            return o1.value-o2.value;
        }
    });
    public static void main(String[] args) {
        // 随机选一个点
        int p = 3;
        tag(p);
        int minLength = 0;
        Line line = null;
        while ((line = queue.poll()) != null){
            // 从优先队列中取出一条最短的边，访问改边的另一个节点A，如果节点A没有访问过，则访问并标记
            if(!tag[line.y]){
                tag(line.y); // 标记访问
                minLength += line.value; // 计算最短路径
                System.out.println(node[line.x]+" "+node[line.y]+" 联通");
            }
        }
        System.out.println(minLength);
    }
    // 标记点已经被访问
    static void tag(int p){
        tag[p]=true;
        for(int i=0;i<node.length;i++){
            // 将该点所连接的边加入到优先队列
            if(map[p][i] != max){
                queue.add(new Line(map[p][i],p,i));
            }
        }
    }
    // 边
    static class Line{
        private int value;
        private int x;
        private int y;
        public Line(int value,int x,int y){
            this.value = value;
            this.x = x;
            this.y = y;
        }
    }
}