数据结构-二叉搜索树的前驱和后继节点
什么是二叉树的前驱节点和后继节点?
某节点的前驱节点的val值小于该节点的val值并且值是最大的那个节点。
某节点的后继节点的val值大于该节点的val值并且值是最小的那个节点。
下面给出一个二叉树节点类,和一个例子来说明。
package com.dzqc.yx.tree;
/**
* 节点类
* @author jiajia
* @param <T>
* @param <E>
*/
public class Node<T,E> {
/**
* 用于查找数据时比较的key
*/
public Integer key;
/**
* 数据
*/
public E e;
/**
* 父节点引用
*/
public Node<T,E> parent;
/**
* 左子节点引用
*/
public Node<T,E> left;
/**
* 右子节点引用
*/
public Node<T,E> right;
public Node(Integer key, E e) {
super();
this.key = key;
this.e = e;
}
public Node(Integer key, E e, Node<T, E> parent) {
super();
this.key = key;
this.e = e;
this.parent = parent;
}
public E setValue(E e) {
return this.e=e;
}
}
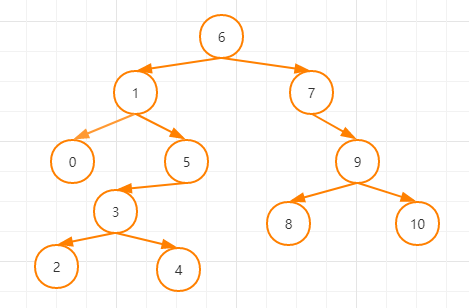
如上图:
1的前驱节点是0,4的前驱节点是3,6的前驱节点是5,3的前驱节点是2.
7的后继节点是8,9的后继节点是10,4的后继节点是5,2的后继节点是3
注意:上述的节点类都有对父节点的引用,如果没有父节点的引用将会用先序遍历的方式求,将会加大时间复杂度。
算法过程
某节点的前驱节点
- 若该节点有左子树,那么该节点的前驱节点是其左子树中val值最大的那个节点。
- 若该节点没有左子树,则判断该节点和其父节点的关系。
- 若该节点是其父节点的右子树,那么该节点的前驱结点就是其父节点。
- 若该节点是其父节点的左子树,那么沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的右子树,那么节点Q就是该节点的后继节点。
某节点的后继节点
- 若该节点有右子树,那么该节点的后继节点是其右子树中val值最小的那个节点。
- 若该节点没有右子树,则判断该节点和其父节点的关系。
- 若该节点是其父节点的左子树,那么该节点的后继结点就是其父节点 。
- 若该节点是其父节点的右子树,那么沿着其父亲节点一直向树的顶端寻找,直到找到一个节点P,P节点是其父节点Q的左子树,那么节点Q就是该节点的后继节点。
java代码实现
前驱节点代码实现
/**
* 寻找前驱节点
* @param t
* @return
*/
public Node<Integer,Integer> precursor(Node<Integer,Integer> t){
if(t!=null) {
if(t.left!=null) {
Node<Integer,Integer> p=t.left;
while(p.right!=null)
p=p.right;
return p;
}else {
if(t==t.parent.right) {
return t.parent;
}else {
Node<Integer,Integer> p=t.parent;
while(p!=null&&p!=p.parent.right) {
p=p.parent;
}
return p.parent;
}
}
}else {
return null;
}
}
前驱节点测试
/**
* 前驱节点
*/
@Test
public void test24() {
Node<Integer,Integer> n6=new Node<>(6,6,null);
Node<Integer,Integer> n1=new Node<>(1,1,n6);
Node<Integer,Integer> n5=new Node<>(5,5,n1);
Node<Integer,Integer> n3=new Node<>(3,3,n5);
Node<Integer,Integer> n2=new Node<>(2,2,n3);
Node<Integer,Integer> n4=new Node<>(4,4,n3);
Node<Integer,Integer> n7=new Node<>(7,7,n6);
Node<Integer,Integer> n9=new Node<>(9,9,n7);
Node<Integer,Integer> n8=new Node<>(8,8,n9);
Node<Integer,Integer> n10=new Node<>(10,10,n9);
n6.left=n1;
n6.right=n7;
n1.right=n5;
n5.left=n3;
n3.left=n2;
n3.right=n4;
n7.right=n9;
n9.left=n8;
n9.right=n10;
System.out.println(precursor(n10).key);
}
后继节点代码实现
/**
* 寻找后继节点
* @param t
* @return
*/
public Node<Integer,Integer> successor(Node<Integer,Integer> t) {
if (t == null)
return null;
else if (t.right != null) {
Node<Integer,Integer> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
Node<Integer,Integer> p = t.parent;
Node<Integer,Integer> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
后继节点测试
/**
* 后继节点
*/
@Test
public void test23() {
Node<Integer,Integer> n6=new Node<>(6,6,null);
Node<Integer,Integer> n1=new Node<>(1,1,n6);
Node<Integer,Integer> n5=new Node<>(5,5,n1);
Node<Integer,Integer> n3=new Node<>(3,3,n5);
Node<Integer,Integer> n2=new Node<>(2,2,n3);
Node<Integer,Integer> n4=new Node<>(4,4,n3);
Node<Integer,Integer> n7=new Node<>(7,7,n6);
Node<Integer,Integer> n9=new Node<>(9,9,n7);
Node<Integer,Integer> n8=new Node<>(8,8,n9);
Node<Integer,Integer> n10=new Node<>(10,10,n9);
n6.left=n1;
n6.right=n7;
n1.right=n5;
n5.left=n3;
n3.left=n2;
n3.right=n4;
n7.right=n9;
n9.left=n8;
n9.right=n10;
System.out.println(successor(n10));
}
猜你喜欢
数据结构与算法
8385
)java代码实现importjava.util.LinkedList;/***二叉树结点类*@author硅谷探秘者(jia)*/classNode{ publicintdata; publicNodele
blog
数据结构-算法-完全二叉树的权值
数据结构与算法
5926
试题描述:思路:用数组表示完全二叉树,用先序遍历的方式遍历每一层的节点,用一个数组储存每一层的和,因为数据规模小于100000所以用一个容量为17的数组即可。计算完每一层的和,再比较层数最小之和最大
数据结构与算法
7665
题目:判断下方两棵二叉树右方的二叉树是否为左方二叉树的子树例1:||/-----------10(10)------\/-------10(10)------\||||/-------5(5
ofc
二叉搜索树中第k小的元素
official
1313
述给定一个二叉搜索树的根节点root,和一个整数k,请你设计一个算法查找其中第k个最小元素(从1开始计数)。示例1输入:root=[3,1,4,null,2],k=1
输出:1示例2输入:root=[5
数据结构与算法
2854
上一篇:广度优先搜索算法(bfs、广搜)java实现-数据结构和算法用邻接矩阵表示图的定点之间的关系如下图数据结构则用邻接矩阵表示为: privatestaticintmap
blog
二叉树删除节点 c++
数据结构与算法
3586
二叉树删除节点c++先看一个简单的树图删除节点是分以下几种情况:1.待删节点为叶子节点:此种情况下直接删除叶子节点即可2.待删节点只有左子树,或只有右子树,那么将左子树或右子树的根节点替换该节点即可
数据结构与算法
2807
广度优先搜索算法(dfs、深搜)java实现-数据结构和算法用邻接矩阵表示图的定点之间的关系如下图的数据结构:则用邻接矩阵表示为: privatestaticintmap[][]={ {0,3,6
blog
数据结构+算法-堆排序
数据结构与算法
4946
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。以最小堆为例下沉操
目录
没有一个冬天不可逾越,没有一个春天不会来临。最慢的步伐不是跬步,而是徘徊,最快的脚步不是冲刺,而是坚持。