本篇文章为红黑树的预备知识，暂且不涉及节点颜色。

二叉树左旋

        左旋的过程是将x的右子树绕x逆时针旋转，使得x的右子树成为x的父节点，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

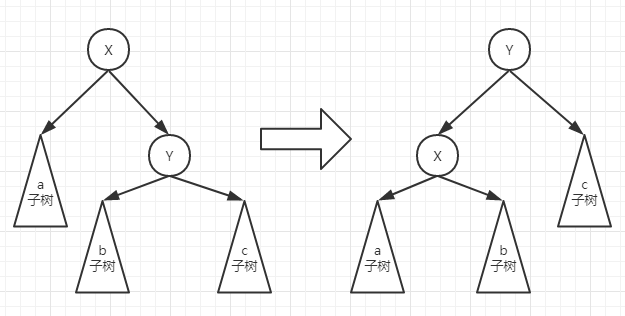
示例：

旋转前

       |                             
/------3(null)-------\               
|                    |               
1(null)       /------10(null)\       
              |              |       
              6(null)        15(null)

旋转后

                     |               
       /-------------10(null)\       
       |                     |       
/------3(null)\              15(null)
|             |                      
1(null)       6(null)                

相关代码：

/**
 * 左旋
 * p为旋转的中心点
 */
public void rotateLeft(Node<T,E> p) {
	if (p != null) {
		Node<T,E> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

二叉树右旋

        右旋的过程是将x的左子树绕x顺时针旋转，使得x的左子树成为x的父节点，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

示例

旋转前

                     |               
       /-------------10(null)\       
       |                     |       
/------3(null)\              15(null)
|             |                      
1(null)       6(null)                

旋转后 

       |                             
/------3(null)-------\               
|                    |               
1(null)       /------10(null)\       
              |              |       
              6(null)        15(null)

相关代码：

/**
 * 右旋
 * 以p点为中心点旋转
 */
public void rotateRight(Node<T,E> p) {
    if (p != null) {
        Node<T,E> l = p.left;
        p.left = l.right;
        if (l.right != null) l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
	}
}

二叉搜索树寻找某节点的前驱节点和后继节点

参考：http://www.jiajiajia.club/official/weblog/39