二叉树基本操作 c++

class node{
public :
	int data;
	node * left;
	node * right;
	node();
	node(int data);
	node(int data,node * left,node * right);
};

#include "node.h"
class trytree{
private:
	node * head;
public:
	trytree();
	void add(int data);//添加二叉树节点
	void preprintf();//先序遍历
	void seqprintf();//中序遍历
	void subprintf();//后序遍历
	void del(int data);
	node * getnode(int data);
};

#include<iostream>
#include"trytree.h"
using namespace std;
node::node(int data){//初始化node节点
	this->data=data;
	this->left=NULL;
	this->right=NULL;
}
node::node(int data,node * left,node * right){
	this->data=data;
	this->left=left;
	this->right=right;
}
trytree::trytree(){//初始化树
	head=NULL;
}
void trytree::add(int data){//添加二叉树节点（easy）
	if(head==NULL){
		head=new node(data);
	}else{
		node * n=head;
		while(n!=NULL){
			if(data<n->data){//向左
				if(n->left!=NULL){//左方不为空
					n=n->left;
				}else{//左方为空
					node * l=new node(data);
					n->left=l;
					return ;
				}
			}else{//向右
				if(n->right!=NULL){
					n=n->right;
				}else{
					node * l=new node(data);
					n->right=l;
					return ;
				}
			}
		}
	}
}
void trytree::del(int data){//删除节点（较为复杂）
	node * n=head;
	node * parent;
	while(n!=NULL){//寻找待删除节点
		if(data>n->data){//向右找
			parent=n;
			n=n->right;
		}else if(data<n->data){//向左找
			parent=n;
			n=n->left;
		}else{//相等即待除节点
			if(n->left!=NULL&&n->right==NULL){//左节点不为空右节点为空
				if(parent->left==n){
					parent->left=n->left;
					delete(n);
					return;
				}else{
					parent->right=n->left;
					delete(n);
					return;
				}
			}else if(n->left==NULL&&n->right!=NULL){//右节点不为空左节点为空
				if(parent->left==n){
					parent->left=n->right;
					delete(n);
					return;
				}else{
					parent->right=n->right;
					delete(n);
					return;
				}
			}else if(n->left==NULL&&n->right==NULL){//待删除的节点为叶子节点
				if(parent->left==n){
					parent->left=NULL;
					delete(n);
					return;
				}else{
					parent->right=NULL;
					delete(n);
					return;
				}
			}else{//左右孩子节点都不为空
				node * sub=n->right;
				if(sub->left==NULL){//sub为后继节点
					sub->left=n->left;
					if(parent->left==n){
						parent->left=sub;
						delete(n);
						return;
					}else{
						parent->right=sub;
						delete(n);
						return;
					}
				}else{
					node * p=sub;//后继节点的父节点
					while(sub->left!=NULL){//寻找后继节点
						p=sub;
						sub=sub->left;
					}
					p->left=NULL;
					if(parent->left==n){
						sub->left=n->left;
						sub->right=n->right;
						parent->left=sub;
						delete(n);
						return;
					}else{
						sub->left=n->left;
						sub->right=n->right;
						parent->right=sub;
						delete(n);
						return;
					}	
				}
			}
		}
	}
	cout<<"没有找到"<<endl;
	return;
}
node * trytree::getnode(int data){
	node * n=head;
	while(n!=NULL){//寻找节点
		if(data>n->data){//向右找
			n=n->right;
		}else if(data<n->data){//向左找
			n=n->left;
		}else{//该节点
			return n;
		}
	}
	return NULL;
}
void pre(node * n){
	if(n==NULL){
		return;
	}
	cout<<n->data<<"  ";
	pre(n->left);
	pre(n->right);
}
void seq(node * n){
	if(n==NULL){
		return;
	}
	seq(n->left);
	cout<<n->data<<"  ";
	seq(n->right);
}
void sub(node * n){
	if(n==NULL){
		return;
	}
	sub(n->left);
	sub(n->right);
	cout<<n->data<<"  ";
}
void trytree::preprintf(){//先序遍历
	cout<<"先序遍历:";
	pre(head);
	cout<<endl;
}
void trytree::seqprintf(){//中序遍历
	cout<<"中序遍历:";
	seq(head);
	cout<<endl;
}
void trytree::subprintf(){//后序遍历
	cout<<"后序遍历:";
	sub(head);
	cout<<endl;
}
int main(){//测试
	trytree * t=new trytree();
	t->add(10);
	t->add(4);
	t->add(20);
	t->add(2);
	t->add(6);
	t->add(15);
	t->add(30);
	t->add(18);
	t->add(25);
	t->del(25);
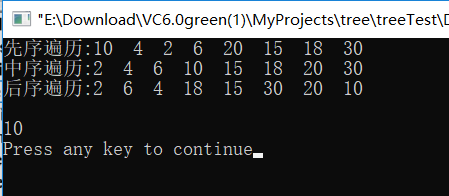
	t->preprintf();
	t->seqprintf();
	t->subprintf();
	cout<<endl;
	cout<<t->getnode(10)->data<<endl;
	return 0;
}