最小生成树Kruskal算法-数据结构和算法
最小生成树算法和其应用
什么是最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
对于任何一个数据结构或算法,理解和实现只是一个方面,更重要的是要明白它的应用范围或应用场景,最小生成树算法的应用非常广泛,例如:
假设要在n个城市之间建立通信联络网,则连接n个城市只需要n-1条线路。这时,自然会考虑这样一个问题,如何在节省费用的前提下建立这个通信网?自然在每两个城市之间都可以设置一条线路,而这相应的就要付出较高的经济代价。n个城市之间最多可以设置n(n-1)/2条线路,使用最小生成树算法就可以在线路中选择出一条总的代价最小的路线。
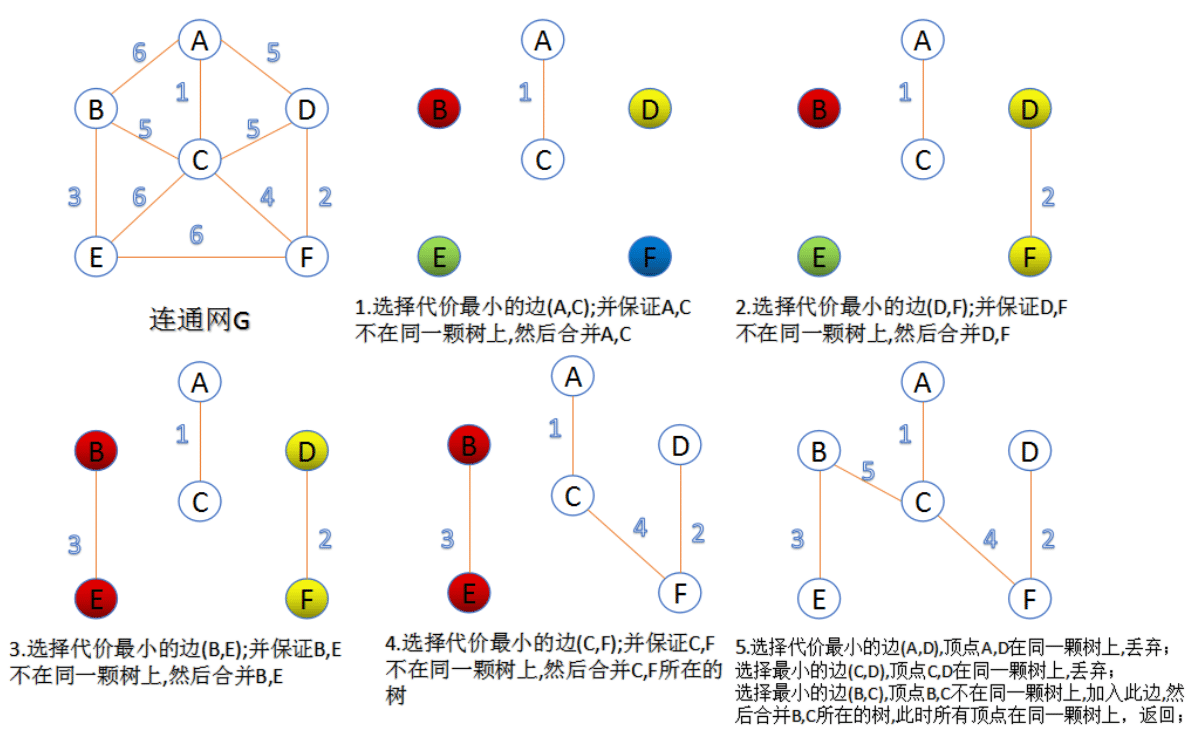
Kruskal算法的算法描述
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
- 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
java代码实现:
我是完全使用了面向对象的思维来设计的这个算法,原因是用面向对象的思维更方便设计。核心代码就七八行
while(lines.size()>0) {
Line l=lines.removeFirst();//从边集合中取出权值最小的一个边
if(!l.node1.tree.set.contains(l.node2)) {//边所在的两个节点是否在同一颗树上(true就是在一棵树上)
ln.add(c[l.node1.node]+"->"+c[l.node2.node]);
for(Node node:l.node1.tree.set) {//把一棵树上的节点全部移动到另外一棵树上(合并为一棵树)
node.tree=l.node2.tree;//修改节点所在的树
l.node2.tree.set.add(node);//加入树的节点集合
}
}
}
完整代码:
package 最小生成树;
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Set;
//节点
class Node{
public Node(int n) {
this.node=n;
}
public int node;//节点
public Tree tree;//节点所在的树
}
//边
class Line implements Comparable<Line>{
public Line(int cost,Node n,Node n2){
this.cost=cost;
this.node1=n;
this.node2=n2;
}
public int cost;//代价
public Node node1;
public Node node2;
@Override
public int compareTo(Line l) {//排序接口
if(this.cost>l.cost) return 1;
else if(this.cost<l.cost) return -1;
return 0;
}
@Override
public String toString() {
return cost+"";
}
}
//树
class Tree{
public Tree(Node n) {
set.add(n);
n.tree=this;
}
public Set<Node> set=new HashSet<Node>();//树的所有节点集合
}
/**
* Kruskal最小生成树算法
* @author LENOVO
*
*/
public class Kruskal {
private static char[] c= {'a','b','c','d','e','f'};
/**
* 连通图表示
*/
private static int[][] map=new int[][]{{0 ,6 ,1 ,5 ,-1,-1},
{6 ,0 ,5 ,-1,3 ,-1},
{1 ,5 ,0 ,5 ,6 ,4 },
{5 ,-1,5 ,0 ,-1,2 },
{-1,3 ,6 ,-1,0 ,6 },
{-1,-1,4 ,2 ,6 ,0 }};
public static void main(String[] args) {
Set<Tree> forest=new HashSet<Tree>();//森林
Node n[]=new Node[map.length];//所有节点集合
for(int i=0;i<map.length;i++) {//生成节点
n[i]=new Node(i);
forest.add(new Tree(n[i]));
}
LinkedList<Line> lines=new LinkedList<Line>();//所有边集合表示
for(int i=1;i<map.length;i++) {//生成边(a-b和b-a是同一个边)
for(int j=0;j<i;j++) {
if(map[i][j]>0) {
lines.add(new Line(map[i][j],n[i],n[j]));
}
}
}
Collections.sort(lines);//边集合从小到大排序
//算法开始
List<String> ln=new ArrayList<String>();
//遍历所有的边集合
while(lines.size()>0) {
Line l=lines.removeFirst();//从边集合中取出权值最小的一个边
if(!l.node1.tree.set.contains(l.node2)) {//边所在的两个节点是否在同一颗树上(true就是在一棵树上)
ln.add(c[l.node1.node]+"->"+c[l.node2.node]);
for(Node node:l.node1.tree.set) {//把一棵树上的节点全部移动到另外一棵树上(合并为一棵树)
node.tree=l.node2.tree;//修改节点所在的树
l.node2.tree.set.add(node);//加入树的节点集合
}
}
}
System.out.println(ln);//最小生成树的边的表示
}
}
评论区
请写下您的评论...
猜你喜欢
数据结构,算法基础
989
[数据结构与算法]
一、什么是最小生成树?二、Kruskal算法三、Prim算法一、什么是最小生成树? 在给定一张无向图,如果在它的子图中,任意两个顶点都是互相连通,并且是一个树结构,那么这棵树叫
blog
数据结构+算法-堆排序
数据结构与算法
4946
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。以最小堆为例下沉操
blog
数据结构-算法-完全二叉树的权值
数据结构与算法
5926
试题描述:思路:用数组表示完全二叉树,用先序遍历的方式遍历每一层的节点,用一个数组储存每一层的和,因为数据规模小于100000所以用一个容量为17的数组即可。计算完每一层的和,再比较层数最小之和最大
blog
选择排序 - 数据结构和算法
数据结构与算法
1488
算法思想:对冒泡排序的一种改进,每次从没有排序的集合a中拿取一个最大或最小的元素,放入有序的集合b中,直到a集合中的元素被取完算法描述:用变量i遍历整个数组,用变量j遍历i后面的数组,每次遍历i初始
blog
程序员必须掌握的数据结构和算法
数据结构与算法
2170
原文链接:https://www.zhihu.com/question/23148377?sort=created算法基础 时间复杂度 空间复杂度基础数据结构 线性表 列表(必学) 链表(必学
数据结构与算法
2808
广度优先搜索算法(dfs、深搜)java实现-数据结构和算法用邻接矩阵表示图的定点之间的关系如下图的数据结构:则用邻接矩阵表示为: privatestaticintmap[][]={ {0,3,6
数据结构与算法
2854
上一篇:广度优先搜索算法(bfs、广搜)java实现-数据结构和算法用邻接矩阵表示图的定点之间的关系如下图数据结构则用邻接矩阵表示为: privatestaticintmap
数据结构与算法
7666
题目:判断下方两棵二叉树右方的二叉树是否为左方二叉树的子树例1:||/-----------10(10)------\/-------10(10)------\||||/-------5(5
最新发表
归档
2018-11
12
2018-12
33
2019-01
28
2019-02
28
2019-03
32
2019-04
27
2019-05
33
2019-06
6
2019-07
12
2019-08
12
2019-09
21
2019-10
8
2019-11
15
2019-12
25
2020-01
9
2020-02
5
2020-03
16
2020-04
4
2020-06
1
2020-07
7
2020-08
13
2020-09
9
2020-10
5
2020-12
3
2021-01
1
2021-02
5
2021-03
7
2021-04
4
2021-05
4
2021-06
1
2021-07
7
2021-08
2
2021-09
8
2021-10
9
2021-11
16
2021-12
14
2022-01
7
2022-05
1
2022-08
3
2022-09
2
2022-10
2
2022-12
5
2023-01
3
2023-02
1
2023-03
4
2023-04
2
2023-06
3
2023-07
4
2023-08
1
2023-10
1
2024-02
1
2024-03
1
2024-04
1
2024-08
1
标签
算法基础
linux
前端
c++
数据结构
框架
数据库
计算机基础
储备知识
java基础
ASM
其他
深入理解java虚拟机
nginx
git
消息中间件
搜索
maven
redis
docker
dubbo
vue
导入导出
软件使用
idea插件
协议
无聊的知识
jenkins
springboot
mqtt协议
keepalived
minio
mysql
ensp
网络基础
xxl-job
rabbitmq
haproxy
srs
音视频
webrtc
javascript
加密算法
目录
没有一个冬天不可逾越,没有一个春天不会来临。最慢的步伐不是跬步,而是徘徊,最快的脚步不是冲刺,而是坚持。